By What Means Can the Internal Energy of a Closed System Increase?
The First Constabulary for Closed Systems
We have already encountered work and heat as two forms of free energy. In order to complete the picture show for closed systems, another type of energy, internal energy, must exist taken into consideration. These 3 forms of energy will afterward be combined in the Kickoff Law of Thermodynamics.
Internal energy
Consider the heating of ane kilogram of Helium in a rigid stationary container from \(300K\) to \(600K\). No work was performed as the volume stayed constant and the system remained stationary. Therefore the energy added to the system every bit oestrus, is captivated past the molecules of the gas. Information technology increased the kinetic free energy of the individual Helium atoms. To name three:26
-
Translational kinetic free energy
-
Rotational kinetic energy
-
Vibrational kinetic free energy
The sum of all these microscopic energies is called the internal energy of a substance. It tin can be shown that specific internal energy is a property. The symbol for specific internal free energy is \(u\) and its units are [\(kJ/kg\)]. The full internal energy of a system is \(U [kJ]\) and is equal to \(m\times u\). Because specific internal energy is a property, it is one of the variables that can be used to fix the state of a substance. For a single stage organization it ways if we know the value of the internal free energy and either the value of temperature or pressure or specific volume, the country is fixed and the value of the other properties can be determined.
The alter in internal energy is calculated using the following equation (Sonntag and Borgnakke 2012 Equation fourteen.30):
\[\brainstorm{equation} du = C_vdT + \left[ T \left(\frac{\fractional P} {\partial T}\right)_v - P\right] dv \tag{4.1} \end{equation}\]
Where \(C_v\) is the abiding volume specific heat. Information technology is divers as the amount of rut necessary to heighten the temperature of a substance (at constant volume) past i caste.
Ideal gases
For an ideal gas it is causeless that the atoms or molecules practice not attract or repulse each other. Therefore in that location is no free energy associated with inter-particle interactions. The distance betwixt particles is therefore irrelevant from an energy bespeak of view. This means that the internal energy of an platonic gas is only made upward of the kinetic energies of private particles and that internal free energy is not influenced by changes in density or pressure. The same is articulate from Equation (4.1). For an ideal gas \(\frac{\partial P} {\fractional T}\) is equal to \(\frac{R}{v}\) and the term in the foursquare brackets reduces to zero. The change in internal free energy for an ideal gas is therefore simply dependent on the change in temperature and can be calculated equally follows:
\[\begin{equation} u_2 - u_1 = \int_{T_1}^{T_2} \! C_{v} \, \mathrm{d} T \tag{four.two} \end{equation}\]
Where \(C_v\) is the constant volume specific rut of the gas which can be a complex office of temperature. To avoid having to integrate Equation (four.2) every time, the internal energy of ideal gases every bit function of temperature (relative to a reference temperature \(T_{ref}\) where the value of \(u_{ref}\) is fix to a chosen value27), is tabulated equally role of temperature.28 A table giving the internal energy of air under the supposition of platonic gas behaviour, is given in Borgnakke and Sonntag, Table A7.1 (Sonntag and Borgnakke 2012).
Instance
Calculate the temperature and specific book of air at \(200kPa\) with a specific internal energy of \(315.64\frac{kJ}{kg}\).
Solution
From the table of the ideal gas backdrop of air (Sonntag and Borgnakke 2012) it can be adamant that the temperature corresponding to the given internal energy is \(440K\). The Ideal Gas Constabulary can at present be used to summate the specific volume: \(0.6314\frac{thou^iii}{kg}\)
Note that because of the assumption of platonic gas behaviour, internal free energy and temperature are no longer independent and both cannot be specified to fix the state of the organisation. Therefore \(u\) can simply exist used in combination with \(P\) and \(v\).
Perfect gases
\(C_v\) for a few gases as function of temperature are shown in Figure four.1.
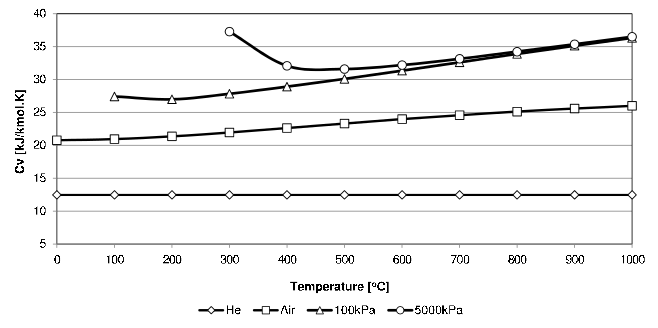
Figure 4.one: \(C_v\) values for Helium, Air and Steam (at 2 pressures).
From Figure four.1 it is clear that the \(C_v\) of Helium stays essentially abiding.29 In this text information technology will be causeless that the \(C_v\) of the mono-diminutive gases (Helium, Argon, Neon and Krypton), is independent of temperature and that they also obey the Ideal Gas Law. They are then collectively called Perfect Gases . For a \(C_v\) independent of temperature, Equation (4.ii) is easily integrated to requite the change in internal energy for perfect gases:
\[\begin{equation} u_2 - u_1 = C_{five} (T_2-T_1) \tag{iv.three} \end{equation}\]
Instance
Helium at \(400kPa\) and \(300^\circ C\) is heated to \(600^\circ C\) while the pressure changes to \(500kPa\). Determine the alter in book and the change in specific internal energy.
Solution Using Equation (4.3) and obtaining the value of \(C_v\) from an appropriate table containing backdrop of Ideal gases (Sonntag and Borgnakke 2012 Tabular array A.five):
\[\begin{aligned} u_2-u_1 &= C_v(T_2-T_1)\\ &= iii.116\times(600-300)\\ &=934.8 \hspace{0.3em} \frac{kJ}{kg}\\ \end{aligned}\]
From the Ideal Gas Police:
\[\begin{aligned} v_2-v_1 &=\frac{R\times T_2}{P_2}-\frac{R\times T_1}{P_1}\\ &=\frac{ii.0771\times873.15}{500}-\frac{2.0771\times573.15}{400}\\ % &=4.534-ii.381\\ &=0.651 \hspace{0.3em} \frac{g^iii}{kg} \\ \finish{aligned}\]
It is important to notation the post-obit:
-
The value for \(C_v\) plant in tables is unremarkably at a specific temperature merely for a Perfect Gas can be used at any temperature because for Perfect Gases it is assumed to be contained of temperature.
-
Even though this is not a constant book process, Equation (4.iii) is still valid. It is valid for any perfect gas for any procedure: isobaric, isochoric, unspecified.… and can be used to calculate the change in internal energy as long equally the modify in temperature is known.
-
For a perfect gas, information technology is only possible to calculate the change in internal energy. This means that the internal energy of a perfect gas does not take a value that can exist used to define the land. For perfect gases it is therefore necessary to employ two of the other 3 intensive properties (\(P, T, v\)) we are familiar with at the moment to define the state.
-
A perfect gas is a special kind of ideal gas, therefore internal energy does not modify with a change in pressure.
-
The temperature difference calculated in \(^\circ C\) is the same as the temperature difference calculated in Kelvin.
-
In the Ideal Gas Police force, the temperature must be in Kelvin.
Real gases
For real gases there are energy associated with inter-particle interactions (attraction or repulsion). Therefore density (and pressure) are important. From Table 4.ane below, the influence of pressure on the internal energy of steam at \(400^\circ\)C is articulate.
| Pressure level (\(kPa\)) | Specific Internal Free energy (\(kJ/kg\)) |
|---|---|
| 10 | 2968.9 |
| 100 | 2967.nine |
| thou | 2957.3 |
| 10000 | 2832.4 |
| 25000 | 2430.one |
Note that at low pressures, internal energy does not vary much with pressure. This is because at depression pressures, the steam molecules are far apart and the energy associated with their interaction, pocket-sized. As the pressure rises to higher values and especially close the disquisitional betoken, internal energy is very sensitive to pressure. For a real gas it is necessary to know the value of two variables to fix the land. Any two of the variables we accept encountered thus far (Temperature, Pressure, specific volume or specific internal energy) can exist used.
Two phase systems
For ii-phase systems, pressure level and temperature are no longer independent. For a saturated liquid (\(x=0\)) and a saturated vapour, (\(10=1\)) the value for internal energy can be read directly from the table for saturated h2o at the appropriate temperature or pressure. Unremarkably the reference point is the internal energy of the saturated liquid at \(0.01^\circ C\) which is taken as nil. However, in that location is no reason why another reference signal may not be chosen.
For a saturated ii-phase mixture, a adding must be done to make up one's mind the value of internal energy for the mixture. Quality (\(x\)) has already been divers as the mass of vapour in a \(1kg\) 2-stage mixture. Quality can now be used to calculate the specific internal energy of a ii-stage mixture from the internal energy of the saturated liquid (\(u_f\)) and the saturated vapour (\(u_g\)) as follows: \[u = (i-x)u_f + xu_g\]
Compressed liquids
The internal energy for compressed (or sub-cooled) liquids equally function of temperature and pressure level tin can be found in the steam tables (Sonntag and Borgnakke 2012 Tabular array B.1.four.) The effect of pressure on the internal energy of liquid water is very small equally shown in Table 4.2 below.
| Force per unit area (\(kPa\)) | Specific Internal Energy (\(kJ/kg\)) | Density (\(kg/yard^3\)) |
|---|---|---|
| 101.325 | 419.0 | 958.4 |
| m.000 | 418.7 | 958.8 |
| 10000.000 | 416.1 | 963.0 |
For a hundred-fold increase in pressure, the internal free energy changes past less that one percentage. This is because the inter-particle distance changes very little every bit tin can exist seen from the modest variation in specific book with the large change in pressure. For incompressible substances, pressure level will not affect inter-particle distances at all and therefore also take no consequence on the internal free energy associated with inter-particle interactions and internal energy. As it is usually assumed that sub-cooled liquids and solids are incompressible, it is as well assumed that their internal energies are not affected by pressure. In this text the internal energy for liquid h2o is therefore causeless to be simply a part of temperature. This means that the internal energy for liquid water tin be read from the tables for saturated liquid h2o. For example the internal energy of water at \(10MPa\) and \(100^\circ C\) is causeless to be equal to the internal energy of saturated liquid water at \(100^\circ C\) fifty-fifty though the saturation pressure level is only \(101.325kPa\).
Solids
Usually constant specific heats are assumed for solids. Then the change in internal free energy can exist calculated using Equation (iv.3). Withal, because of the small change in volume during heating, the values of \(C_v\) and \(C_p\) are substantially equal and oftentimes no distinction is made betwixt the two or only \(C_p\) is tabulated. This is discussed in more than detail in Paragraph 5.4.1.
Determination of internal energy
One time the value of two independent properties are known the state is fixed and the value of the other properties tin can be adamant30. Let us consider a few examples involving internal energy.
Temperature and pressure.
The three phases of h2o every bit role of force per unit area and temperature are shown in Effigy 2.2. The first footstep is to make up one's mind the phase as explained in Paragraph 2.4.1 by determining the position of the land relative to the stage boundaries.
Case
Determine the specific internal energy and specific volume of h2o at \(100kPa\) and \(50^\circ C\).
Solution
From the position on the phase diagram (\(\Box\) in Figure 2.2), it is articulate that it is a compressed liquid. Assuming that \(u_{T,P}=u_{f_{sat@T}}\): \(u=209.3\frac{kJ}{kg}\) and as well for specific volume, \(5=0.001012\frac{1000^3}{kg}\). Quality is not divers for a compressed liquid.
Case
Determine the specific internal energy and specific book of water at \(100kPa\) and \(150^\circ C\).
Solution
The state is indicated by the \(\circ\) in Figure two.ii. From the position on the phase diagram, information technology is clear that it is a super-heated vapour. From the tables for super-heated water vapour, we tin can read the values for \(u=2582.75\frac{kJ}{kg}\) and \(5=i.93636\frac{m^3}{kg}\). Quality is not defined for a super-heated vapour.
Note that on a P-T diagram, the state can never prevarication on the line separating the phases. The line has zero thickness and therefore, for a specific temperature and pressure, the phase will be either a liquid or a vapour.
Temperature or pressure and internal energy
The stage is adamant by comparing the internal energy of the system with the internal energy of the saturated vapour and saturated liquid at the specified pressure or temperature. If the specified value for internal free energy falls inside the dome , information technology is a two phase mixture and the temperature is the saturation temperature. The quality can now be determined and from the quality, the specific volume.
Figure four.2: Phase diagram for water.
Example
Determine the temperature, specific volume and quality of water at \(200kPa\) with an internal free energy of \(2808.6kJ/kg\).
Solution
The specified internal energy is bigger than the internal free energy of saturated vapour at \(200kPa\), \(2529\frac{kJ}{kg}\) and therefore it is a super-heated vapour. From the tables for super-heated water vapour at \(200kPa\), the temperature that corresponds with the specified internal free energy, is \(300^\circ C\). The specific book is \(1.31616\frac{m^three}{kg}\). Quality is not defined for a super-heated vapour.
Case
Calculate the internal energy at \(100kPa\) of a 2-phase water mixture with a quality of \(0.2\). (\(835.1kJ/kg\))
Example
Determine the pressure of steam at \(200^\circ C\) with an internal energy of 2656
Solution
The specified value for internal energy is bigger than than the internal free energy of saturated vapour at \(200^\circ C\), \(2595\frac{kJ}{kg}\) and information technology is therefore a super-heated vapour. From the tables for super-heated steam, it is clear that the internal free energy of steam at \(200^\circ C\) and \(100kPa\) is bigger; and the internal energy at \(200^\circ C\) and \(200kPa\) smaller than the specified value, 2656. The pressure of the system must therefore be between \(100kPa\) and \(200kPa\). Interpolation is therefore required. (\(156kPa\)).
The Beginning Law for airtight systems
The Kickoff Law only states that energy cannot exist destroyed or created — only converted from 1 course to some other. In a coal fired power station, estrus is converted into piece of work and electricity. The Get-go Constabulary gives the relation between the three forms of energy encountered and then far - estrus, work and internal free energy. Consider the closed arrangement in Figure 4.3 undergoing a procedure. Usually the substance contained in the piston-cylinder organisation is taken as the system. Oestrus is added to the system, it expands and raises the piston, performing work.
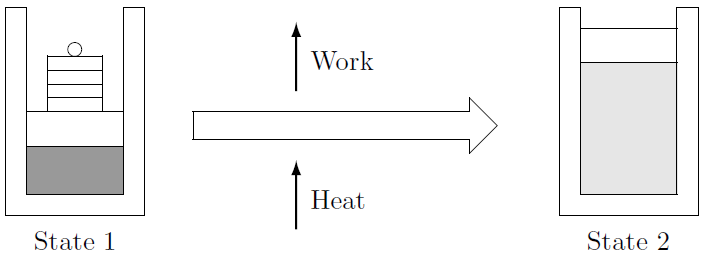
Figure iv.3: Airtight arrangement undergoing a process.
The First Law states that energy is conserved. This ways that the amount of energy in the beginning, the total internal energy \(U_1\), plus the amount of energy transferred to the system, the rut \(Q_{in}\), must equal the the piece of work washed past the system, \(W_{out}\), plus the corporeality of energy in the system at the end of the process, the total internal energy \(U_2\). In mathematical terms: \[U_1 + Q_{in} = W_{out} + U_2\] or: \[yard u_1 + Q_{in} = m u_2 + W_{out}\] It is important to note that the formulation of the Start Law hither deals with the corporeality (or quantity) of energy. The units are kilo-Joule or [\(kJ\)]. 31
Example
Ane kilogram of steam in a piston-cylinder arrangement is at \(200^\circ C\) and \(300kPa\). The steam is heated to \(400^\circ C\) in a constant force per unit area procedure. Calculate the heat that must exist added in order for the process to have place equally described.
Solution
The Start Law is rearranged: \(Q_{in} = grand(u_2 -u_1) + W_{out}\)
The work performed in a constant pressure process: \[W_{out}=P(V_2-V_1)=300(1.03151-0.71629)=94.57kJ \Rightarrow Washed\hspace{0.5em} by \hspace{0.5em}system\]
The First Law now becomes:\[Q_{in}=(2965.53-2650.65)+94.57=409.45kJ \Rightarrow Required\hspace{0.5em} past\hspace{0.5em} organisation\] Note that less than 25% of the free energy added every bit heat is converted into piece of work.
Kinetic and potential energy
Whereas internal free energy is on a microscopic level, the system tin also undergo changes in energy on a macroscopic level. If the center of gravity of the organisation changes height in a gravitational field or changes velocity considering of interactions between the organization and the environment, the energy associated with these changes must be taken into consideration and the Kickoff Law becomes: (Annotation that the kinetic free energy (\(\frac{1}{ii}g\overline Five^2\)) and potential energy (\(mgZ\)) terms are divided by 1000 to ensure their units are in \(kJ\)). \[Q_{in} = U_2 - U_1 + \frac{m(\overline{V}_2^2 - \overline{Five}_1^2)}{2000} + \frac{mg(Z_2-Z_1)}{yard} + {W_{out}}\] where \(\overline{V}\) is the velocity of the center of gravity of the system (in \(m/s\)) and \(Z\) is the pinnacle of the center of gravity of the system (in meters). Ordinarily the changes in kinetic and potential energy are much smaller than the other terms and tin safely be ignored. But there are instances where information technology must be taken in to consideration:
Instance
In a paint ball gun, the ball (mass: \(three one thousand\)) is propelled by a fixed amount of high pressure air with an initial pressure level of \(5000 kPa\). Due to the pressure level difference across the ball, it accelerates until information technology leaves the barrel. Let u.s.a. calculate the velocity of the paintball every bit information technology leaves the butt. The internal energy of the pressurized air provides the energy necessary to accelerate the paint brawl and push away the atmospheric air. An energy balance becomes: \[m_a u_1=m_a u_2 + W_{atm} + \frac{m_{lead}\overline{V}^2}{2000}\] The pressure at the front end of the pigment ball is equal to atmospheric. The work necessary to push away the temper is: \[W_{atm}=P_{atm}(V_1-V_2)\] The initial volume of the pressurized air (assume a mass of \(0.4 g\) of pressurized air): \[V_1=\frac{mRT_1}{P_1}=\frac{4\times 10^{-iv}\times 0.287\times 298.15}{5000}=vi.85\times x^{-half-dozen}chiliad^3\] Assume the pressurized air expands to 36 times its initial volume and that \(P_{atm}=87kPa\). So \(W_{atm}=0.0209 kJ\). Furthermore, permit us assume air is a perfect gas and that it expands adiabatically. For an initial air temperature of \(25^\circ C\) the terminal temperature can be calculated (Paragraph 4.three): \[T_2=T_1\left(\frac{V^two}{Five^1}\right)^{one-thou}=71K\] This means: \[m_{a}(u_1-u_2)=m_{a}C_{five}(T_1-T_2)=0.0651kJ\] Therefore, the velocity of the paint brawl when it leaves the barrel: \[\overline{V}=\left(2000 \times \frac{0.0651-0.0209}{0.003}\correct)^{0.5}=171.7\frac{thou}{s}\] Annotation that the (adiabatic) work done by the air on the paint ball will be more than that the free energy necessary to push abroad the atmosphere. The adiabatic piece of work done by the air, minus the work necessary to push away the atmosphere, volition be equal to the alter in kinetic energy of the paint ball. It is left to the reader to calculate the adiabatic piece of work performed by the expanding air and evidence that the numeric value of the adiabatic work is equal to the modify in the internal energy of the air.
In our calculations, we ignored the kinetic energy of the pressurized air in the butt as the paint ball leaves the barrel. A good assumption is to presume that as the brawl leaves the barrel, that the centre of gravity of the air in the barrel will motility at half the velocity of the paint ball: \(\overline{V}_{air}= 0.5\overline {V}_{ball}\) and include the final kinetic energy of the air in the energy remainder. This volition reduce the calculated velocity of the paint ball to \(166\frac{m}{south}\).
The calculations in a higher place we causeless a reversible (platonic) procedure which yielded the theoretical maximum velocity. The actual velocity of a paint ball is approximately \(90\frac{m}{s}\) due to not-idealities such as friction.
Allow us consider potential energy:
Example
A vertical piston/cylinder arrangement with a cross sectional area of \(0.002m^2\) (\(D=fifty.46 \hspace{0.1em} mm\)) contains \(1kg\) saturated liquid h2o at \(100kPa\). The water is vaporised at constant pressure until saturated vapour results. Calculate the heat required.
Solution
The elevation of the column of the liquid water will be \(0.521m\) and the acme of the vapour column volition be \(846m\). The center of gravity in each case is \(height/2\). The prepare-up is stationary and then the kinetic energy does not change and the Showtime Law becomes:
\[\begin{aligned} Q_{in} &= one thousand\left((u_2-u_1) + g\frac{Z_2-Z_1}{1000}+P(v_2-v_1)\right)\\ &= (2506.06-417.3) + ix.81\frac{846-0.521}{2\times one thousand}+100(1.693-0.001)\\ &= 2088.7 + four.147 + 169.ii \\ &=2262kJ \terminate{aligned}\]
It is articulate that even with this extreme modify in elevation of the eye of gravity, that the contribution of the modify in potential energy is nonetheless small relative to the other terms.
Sign convention
Equation (3.i) gives the piece of work done by a system undergoing a process from state i to state 2:
\[W_{out} = \int_{V_1}^{V_2} \! P \, \mathrm{d} V\]
Because the pressure in the equation in a higher place is the absolute force per unit area, it is always greater (or equal) to null. If the volume increases, work is done Past the system and the value of \(W_{out}\) will be \(>0\). Yet, if work is done ON the arrangement, the book will decrease and the value of \(W_{out}\) volition exist \(<0\). In such cases, this text, in order to take a positive numerical value, the subscript "out" will be changed to "in" ensure that the numerical value is \(>0\).
The heat necessary to heat an ideal gas in a constant volume process from \(T_1\) to \(T_2\), is given by:
\[Q_{in}=m \int^{T_2}_{T_1} C_v dT\]
If heat is added to the system, the temperature will rising and \(T_2>T_1\) and the value of \(Q_{in}\) will be \(>0\). However, if oestrus is released by the system, \(T_2<T_1\) and the value of \(Q_{in}\) will be \(<0\). This is true non simply for constant volume processes, simply for other processes too. In this text the appropriate subscript (\({``in"}\) or \({``out"}\)) volition be used to ensure that the value of \(Q\) is always \(>0\).
Adiabatic processes
The first police can exist used to derive Equation (iii.3) for an adiabatic quasi-equilibrium process for a perfect gas. \[PV^k = c\] which is the same as: \[\frac{P_2}{P_1} = \left(\frac{V_1}{V_2}\right)^thou\]
Now for the derivation. The first police force in differential form: \[\delta{Q} = dU + \delta{W}\] For an adiabatic process \(\delta{Q}=0\), for an ideal gas, \(dU=mC_vdT\) and for a quasi-equilibrium process, \(\delta{W}=PdV\). This gives: \[mC_vdT = -PdV\]
Dividing the left paw side of the equation by \(mRT\) and the correct mitt side by \(PV\), the following equation results for a Perfect Gas:
\[\frac{C_v}{R} \ln \frac{T_2}{T_1} = \ln \frac{V_1}{V_2}\]
Which can be written as:
\[\left(\frac{T_2}{T_1}\correct)^{\frac{C_v}{R}} = \frac{V_1}{V_2}\]
From the Ideal Gas Constabulary it follows that:
\[\frac{T_2}{T_1} = \frac{P_2}{P_1}\frac{V_2}{V_1}\]
The final 2 equations can be combined to give:
\[\frac{P_2}{P_1} ^ {\frac{C_v}{R}} = \frac{V_1}{V_2} ^{ \left( \frac{C_v}{R}+1 \correct)}\]
Noting that that \(C_p-C_v=R\) and after some manipulation, the post-obit equation results: \[\frac{P_2}{P_1} = \left( \frac{V_1}{V_2} \right)^{\frac{C_p}{C_v}} = \left(\frac{V_1}{V_2}\right)^chiliad\]
which is the equation nosotros set out to derive. From the above it also follows that: \[\begin{equation} \frac{T_2}{T_1}=\left( \frac{P_2}{P_1} \correct)^{\frac{thousand-1}{grand}}=\left( \frac{V_2}{V_1} \right)^{one-k}=\left( \frac{v_2}{v_1} \right)^{ane-k} \tag{4.4} \end{equation}\]
millerlecladmands.blogspot.com
Source: https://bookdown.org/asvn90/Understanding-Thermodynamics/the-first-law-for-closed-systems.html
0 Response to "By What Means Can the Internal Energy of a Closed System Increase?"
Post a Comment